Теория Измерения Решения
(Лоуренс М. Раднер)
Разработка под названием Вейлд (Wald) (1947), впервые применена для измерения Кронбахом и Глезером (1957), и в данное время широко используется в машиностроении, сельском хозяйстве и вычислительной технике.
Теории принятия решений для анализа упорядоченных данных, обеспечивают простую модель. Это наиболее актуально в измерениях, когда цель лежит в классификации испытанных одной из двух категорий, например: прошел/провалился, мастер/не мастер.
От пилотного тестирования, к единственной оценке
1. Часть мастера и не мастера в популяции, и
2. Условные вероятности испытуемых в каждой области мастерства, правильно ответивших на каждой позиции.
Этот учебник содержит обзор теории измерения принятия решений. Ключевые понятия будут проиллюстрированы с помощью двоичной классификации (прошел / не прошел) тестирования и образец теста на три пункта. Интерактивный инструмент также предоставляет предложенные вопросы и ответы, которые помогут вам лучше понять, что вы рассматривали. Инструмент использует Java, JavaScript и Cascade Style Sheets и был разработан с использованием Internet Explorer. Это прекрасно работает и с AOL 7.0.
Потребность
Классическая теория измерения и элемент теории ответа обеспокоены, в первую очередь, степенью последовательности испытуемых через способность континуума. Эти модели обеспокоены, например, дифференциацией испытуемых на 90-й и 92-й процентилиями. Но часто заинтересованы в классификации испытуемых в одну из конечного числа дискретных категорий, таких как прошел / не прошел или опытный / начальный / ниже начального. Это проще, результат и более простая модель измерения должна быть достаточной. Теория — Решение — Измерение являются простейшими инструментами.
Теория принятия измеряемых решений требует только одного ключевого предположения — детали являются независимыми. Таким образом, тестируемый домен не должен быть одномерным, способности испытуемого не должны быть нормально распределены, и не нужно иметь дело с подгонкой данных к теоретической модели, как и в пунктах теории ответа (IRT) или в большинстве скрытых моделей. Модель привлекательна в качестве механизма маршрутизации для интеллектуальных обучающих систем, для отслуживших экзаменов, для адаптивного тестирования, и как средство быстро получать классификационные пропорции на других экзаменах. Учитывая эти привлекательные черты, это удивительно, что эта модель не привлекает широкое внимание в рамках сообщества измерений.
Изолированные элементы теории принятия решений появились спорадически в измерительной литературе. Основные статьи в литературе мастерства тестирования 1970-х годов, заняты теорией принятия решений (Hambleton и Novick, 1973; Huynh, 1976; ван дер Линден и Меленберг, 1977) и должны быть пересмотрены в свете измерения сегодняшних проблем. Льюис и Шихан (1990) и другие использовали теорию принятия адаптивно, выбирая отдельные пункты. Кингсбери и Вайс (1983), Reckase (1983), и Спрей и Рикейс (1996) использовали теорию принятия для определения прекращения тестирования.
Теория
Обзор и обозначения
Цель состоит в том, чтобы сформировать лучшее предположение относительно области мастерства (классификация) отдельного испытуемого, на основе ответов испытуемого в пунктах: пункта априорной информации и пропорции априорной классификации населения. Таким образом, модель состоит из четырех компонентов: 1) возможных состояний мастерства для экзаменуемого; 2) калиброванных элементов; 3) шаблонов ответа индивидуума; и 4) решений, которые могут быть образованы у испытуемого.
Есть «К» возможных состояний мастерства, что принимает значение mk. В случае тестирования прошел / провалился, есть два возможных состояния и К = 2. Один, как правило, известен априори, приближенные пропорции для населения всех испытуемых в каждой области мастерства.
Второй компонент представляет собой набор элементов, для которых вероятность каждого возможного наблюдения, априори, — «правильно или неправильно», учитывая область мастерства.
Ответы набора «N» элементов образуют третий компонент. Каждый элемент считается дискретной случайной величины, стохастически связанной с мастерством и реализующейся наблюдаемыми значениями «zN». Каждый испытуемый имеет вектор ответа, z, состоящего из z1, z2, … zN. В этой статье рассматриваются только дихотомически набранные пункты.
Последний компонент является решением пространства. Можно сформировать любое количество D решений, основанных на данных. Как правило, один хочет угадать уровень искусности и это можно определить как D = K. При адаптивном или последовательном тестированием, решение будет продолжать тестировать, будет добавлено тестирование D = К 1. Каждое решение будет обозначаться DK.
Тестирование начинается с доли испытуемых в популяции, которые находятся в каждой из категорий К и доли испытуемых с каждой категории, которые отвечают правильно. Пропорции населения могут быть определены различными способами, в том числе, из предварительного тестирования, преобразований существующих оценок, классификаций и суждений. После того, как эти наборы настоятелей становятся доступными вводятся элементы ( z1, z2, … Zn).
Пропорции от пилотного тестирования рассматриваются и используются как следующие обозначения:
Априорные
р (mk) — вероятность того, что случайно выбранный испытуемый, может оказаться мастером;
р (zn | mk) — вероятность ответа zn учитывая мастерство;
Наблюдения
z- реакция вектор реакции индивида z1, z2, …, zN, где zi — 0 (0,1);
Оценка состояния мастерства обследуемого формируется с помощью априори и наблюдений. По теореме Байеса,
P(mk|z ) = c P (mk|z)P(mk) (1)
Есть вероятность Р (mk|z), что испытуемый является мастером своей области, mk учитывает его вектор ответа равного произведению нормирующей постоянной (с), вероятность вектора ответа учитывается mk и априорной вероятностью классификации. Для каждого испытуемого, есть вероятность К, один для каждого состояния мастерства. Нормировочная константа в (1),
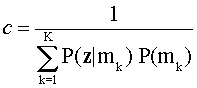
гарантирует, что сумма апостериорных вероятностей равна 1,0.
Предполагаемая местная независимость,
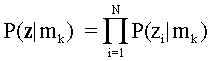 (2)
(2)
То есть, вероятность вектора отклика равна произведению условных вероятностей элементов ответа. В этом уроке, каждый ответ является правильным (1) or wrong (0) and P(z1=0|mk) = 1- P(z1=1|mk).
Три ключевых понятия из теории принятия решений:
1. правила принятия решений
2. последовательное тестирование
3. последовательные решения ;
Модель показана здесь, с рассмотрения двух возможных областей мастерства M1 и M2 и двух возможных решений D1 и D2, является правильным решением для M1 и M2 соответственно. Вектор ответа испытуемого равняется [1,1,0].
Правила принятия решений
Задача состоит в том, чтобы сделать лучшее предположение относительно классификации испытуемого (мастер/ не мастер) и вектора ответа у испытуемого.
Достаточной статистикой для принятия решений является вероятность соотношения
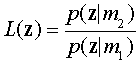
Как пример: L (г) = .09/.19 = 0,47. Что является достаточной статистикой, так как все правила принятия решений можно рассматривать как тест по сравнению L (г) против заданного критерия 8.
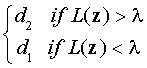 (3)
(3)
Критерий максимально правдоподобного решения
Простой подход для решения и он основывается исключительно на условных вероятностях векторов реагирования данных каждой области мастерства: P(z|m1) and P(z|m2). Концепция заключается в выборе искусности состояния, которое является наиболее вероятной причиной ответа вектора и его можно сформулировать как:
Учитывая набор ответов на вопросы z, примите решение DK, если оно предпочтительней, чем mk генерируемое z.
По этому критерию, можно было бы классифицировать обследуемого как мастера – это наиболее вероятная классификация, начиная от P(z|m1)=.68 > P(z|m2)=.32.
Это равносильно предположению, что априори совпадают. Пример: несколько испытуемых являются мастерами, P (тк) = 0,20. Учитывая, что условные вероятности векторов реагирования довольно близки, это правило классификации может не привести к хорошим результатам.
Минимальная вероятность ошибки решения
Если человек думает о m1 как о нулевой гипотезе, то с точки зрения статистической теории, есть вероятность принятия человека как мастера, а d1, когда на самом деле этот человек не является мастером м2, это знак уровня значимости, а Р (.. d2 | м2) — сила теста.
Учитывая набор ответов на вопросы z, выберите решающие области, которые минимизируют общую вероятность ошибки.
Этот критерий иногда называют критерием идеального наблюдателя. В двоичном случае, Ре = P (d2 | m1) + P (d1 | м2), а соотношение вероятности теста (3) используется с
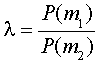
Например, 8 = 25, решение d2 – не мастер.
Максимальный критерий апостериорного (MAP) решения
Критерий вероятности максимального решения использовали только из вероятностей ответа вектора. Минимальная вероятность критерия ошибки также использована для предварительной классификации вероятностей P (m1) и P (м2). MAP — другой подход, который использует имеющуюся информацию.
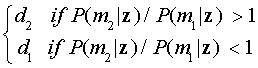
Критерии риска Байеса
Существенным преимуществом в рамках теории принятия решений является то, что можно включать принятие затрат в анализ. По этим критериям, затраты ассигнируются на каждого правильным и неправильным решением, а затем минимизируется суммарные средние затраты.
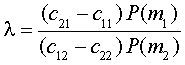 (4)
(4)
Адаптивное тестирование
Вместо того чтобы принять решение о классификации личности после введения фиксированного количества элементов, можно последовательно выбирать элементы, чтобы максимизировать информацию, обновлять расчетные вероятности классификации областей мастерства, а затем оценить, есть ли достаточно информации, чтобы прекратить тестирование. В статистике это называется последовательное тестирование.
![]() (5)
(5)
Минимальная ожидаемая стоимость
Такой подход определяет оптимальный параметр, чтобы быть введенным рядом как элемент с минимально возможной стоимостью. Уравнение обеспечивает решение стоимости в зависимости от вероятностей классификации.
Если c11=c22=0 , то
B=c21 P(d2|m1) P(m1) + c12 P(d1|m2) P(m2) (6)
Информационное усиление
Весь этот очерк обеспокоен использованием предварительного пункта и распределения испытуемой информации в декодировании векторов, чтобы сделать лучшее предположение относительно состояний испытуемых. Часто используемый измеритель информации из теории информации (см. Кавер и Томас, 1991), Шеннон (1948) энтропия, применим здесь:
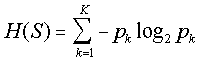 (5)
(5)
H(S0) — H(Si) (6)
![]() (7)
(7)
Последовательные Решения
В этой статье обсуждаются процедуры для принятия решения и процедуры отбора следующих пунктов, которые будут вводиться последовательно. Можно было бы сделать это определение после каждого ответа.
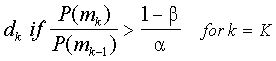
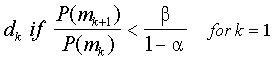
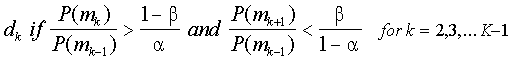
Обсуждение
В своем введении, Кронбах и Глезер (1957) утверждают, что конечная цель для тестирования является достижение качественных решений классификации. Сегодняшние решения часто двоичные: нанимают ли кого-то, осваивает ли человек определенный набор навыков или это касается продвижения индивидуума. Мульти областные условия распространены в областных оценках, например, процент студентов, которые выполняют задания как пользователи базового, опытного или продвинутого уровня. Простая модель измерения, представленная в этой статье, применима к этим и другим ситуациях, когда кто-то заинтересован в информации по категориям.
Эта статья рассматривает два пути адаптивно, администрируя пункты с помощью модели. Традиционная теория принятия решений с последовательным подходом к проведению испытаний, минимальная стоимость, и новый подход, прирост информации, основаны на энтропии и происходят от теории информации.
Научно-исследовательские вопросы многочисленны. Как модель распространяется многократно, а не по дихотомическим пунктам категорий? Как смещения могут быть обнаружены? Насколько эффективно адаптивное тестирование и последовательные правила принятия решений? Может ли модель быть эффективно продлена до 30 или более категорий и обеспечивать ранжирование испытуемых? Как мы можем эффективно использовать тот факт, что данные упорядочены? Как понятие энтропии может быть использовано при рассмотрении тестов? Как модель будет лучше всего применять критерии тестов, оценивающие различные навыки, каждый с небольшим числом предметов? Как различные структуры затрат эффективно используются? Как элементы из одного теста можно выгодно использовать в другом? Как можно уравнять такие испытания? Автор в настоящее время расследует применимость модели к компьютерному озвучиванию эссе.
Примечание
Данное руководство было разработано с помощью финансирования Национальной библиотеки образования, Министерства образования США, «решение ххх и из» Национального института успеваемости учащихся, учебного плана и оценки Министерства образования США и предоставления гранта R305T010130. Взгляды и мнения, высказанные в данной статье, принадлежат автору и не обязательно отражают точку зрения финансирующей организации.
Оригинал статьи — http://echo.edres.org:8080/mdt/